Score base diffusion models

2025年9月12日

14:44

参考视频 ：https://www.youtube.com/watch?v=lUljxdkolK8

 

 

从另一个角度，另一种数学框架，来看扩散过程。

随机可微方程SDE：dx=f(x,t)dt + g(t)dW，其中f(x,t)是确定的，被称为drift，即漂流的大方向。而dW是不确定的，随机的抖动，g(t)表示抖动的强度,被称为diffusion coefficients。

1）可微表现在：it relates variable x to its change over time t

2)  随机表现在：第二项是一个布朗运动，which is random。

 

现在来看DDPM对应的drift和diffusion cofficients的具体形式是什么。

 

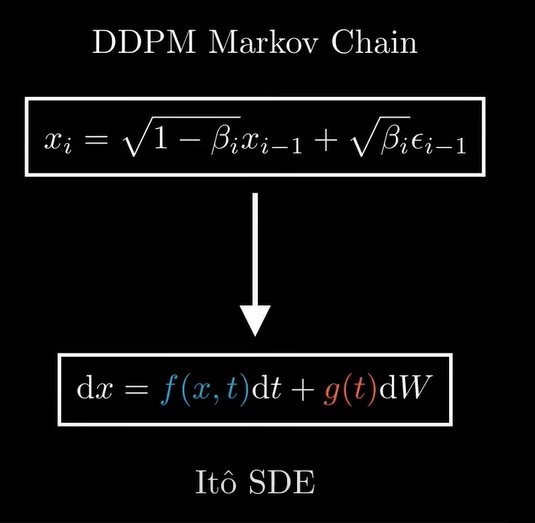
推导过程省略，最后的结果如下图所示

 

其中，dW =

 

这个式子的物理意义是，第一项drift term 的作用是 pulls datapoints to the origin,第二项diffusion term的作用是spreads them out, preventing datapoints from collapsing to a single point.这和我们DDPM中的前向过程是一样的：将任意图片变成完全噪声图片（将任一原始分布变成高斯分布）。

 

 

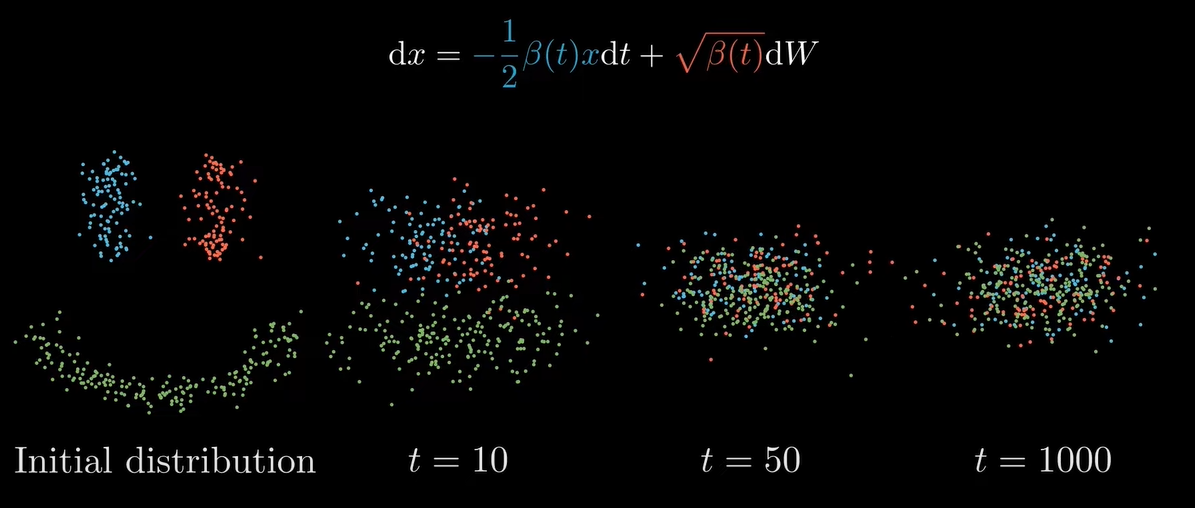
那么，如果我们可以reverse 这个SDE方程，我们就能从噪声图像中恢复原始图像了。上世纪80年代的工作告诉我们，under mild conditions, any forward SDE has a corresponding reverse SDE。

 

 

在上图的式子中，我们唯一不知道的是紫色那一项，，即得分函数score functions，什么是score funcitons呢？

假设有一个分布，样本集中分布在紫色区域，这个分布的score function is a function that assigns to every point in space  a

 vector pointing toward regions of higher porbability. In other words, it tells us which direction the density increases

fastest. 可以把score function比作为一个罗盘，总是指向高密度区域。

 

 

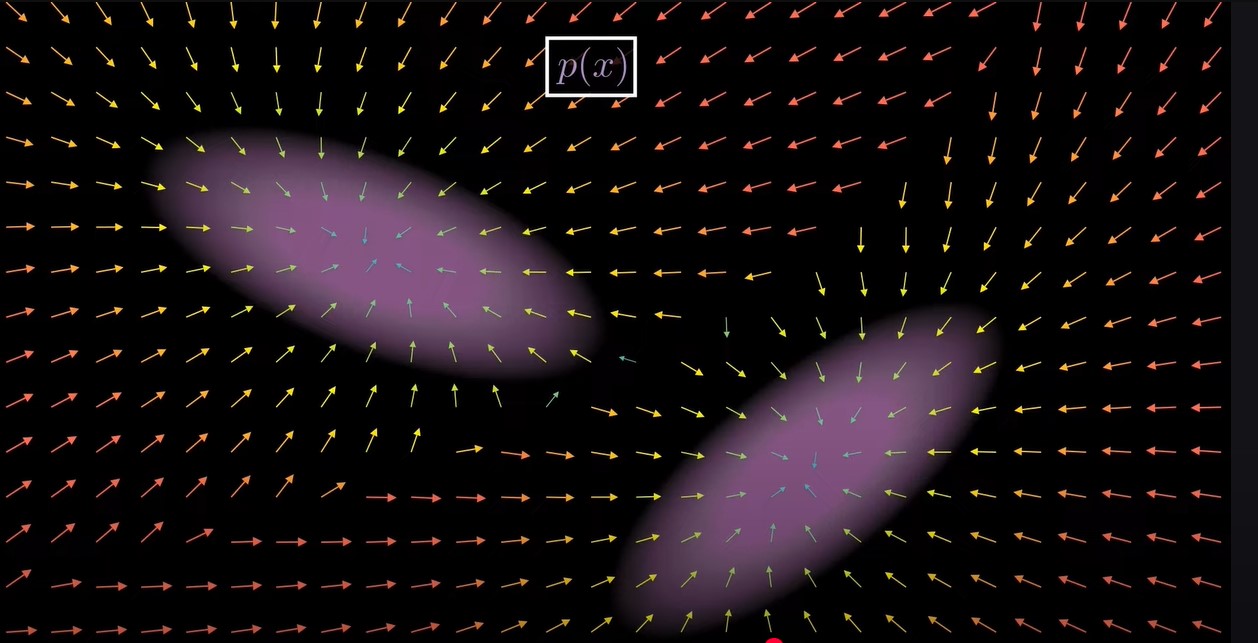
在diffusion刚开始的阶段，由于原始分布没有经过太多的扰动，分布是很clean的，此时score funtion也是sharp的，如上图所示。而随着diffusion的进行（加入越来越多的noise），分布越来越像高斯分布，score funtion也变得smooth了，如下图所示。

 

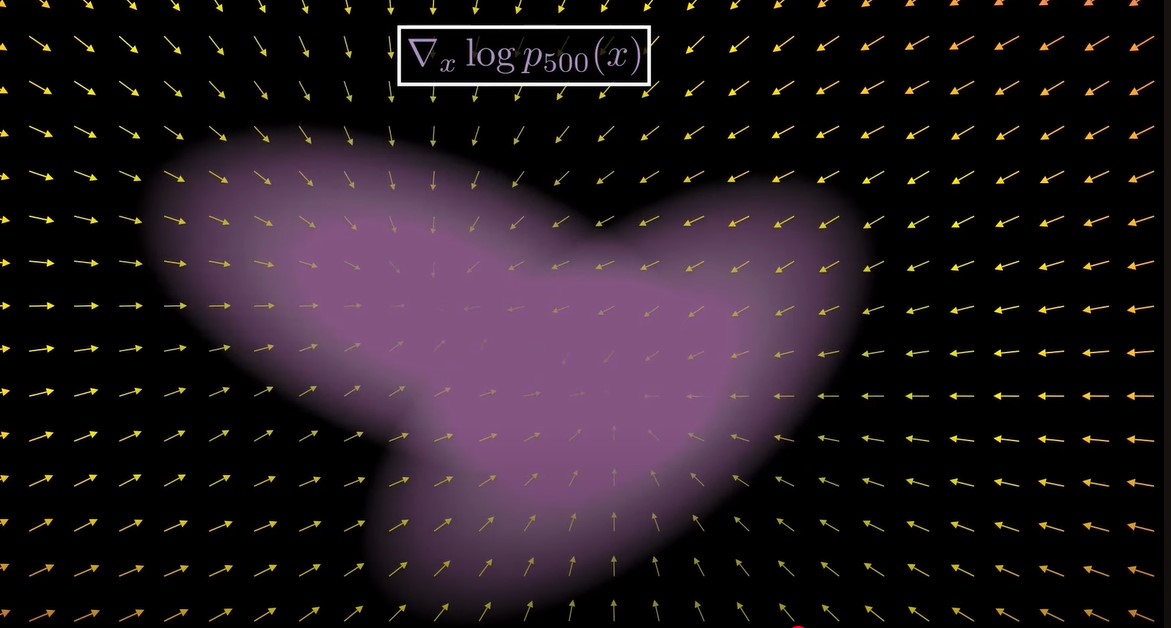
我们需要得到每一步的score function才能reverse SDE，我们用神经网络来学习。神经网络通常是Unet，输入是xt，和t，输出是此时的score funtion。

 

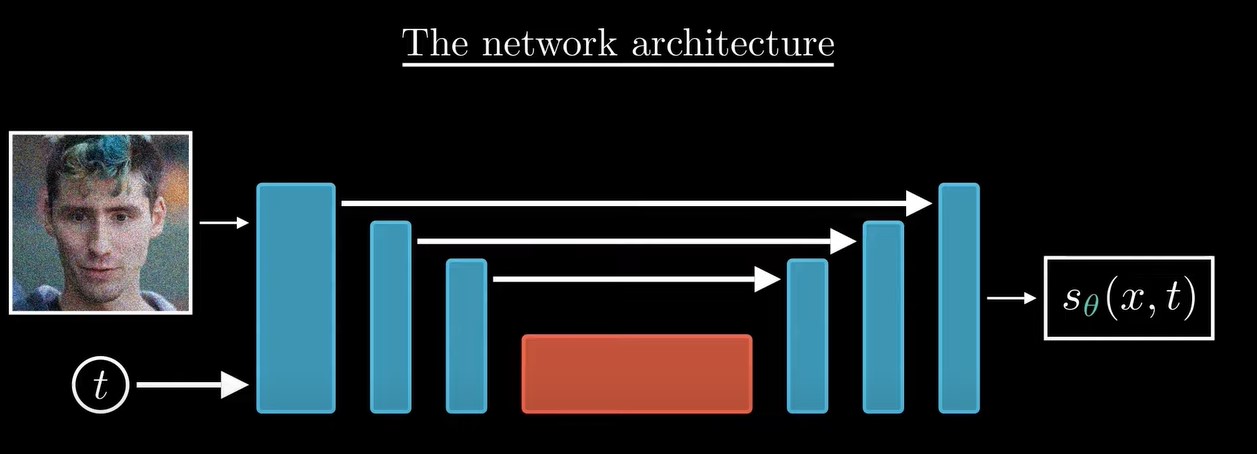
训练的目标就是，我们想让Unet输出的score function和真实的score function越接近越好：

 

其中，，具体推导省略。

 

从上图中看出，DDPM和score match 这两种方法的loss是不同的，因为DDPM是预测每一步的噪声，score match预测的是每一步的score Function。但是这两种方法都可以用来生成新的样本。

 

最后，有了score function之后 ，也就有了reverse SDE方程，但是reverse SDE方程是连续的形式，我们需要对其进行离散化来生成新图片，离散化有很多方法，是一个被广泛研究的领域，最常用的是Euler-Maruyama离散化，

 

总结下DDPM和score match 这两种方法的不同

 

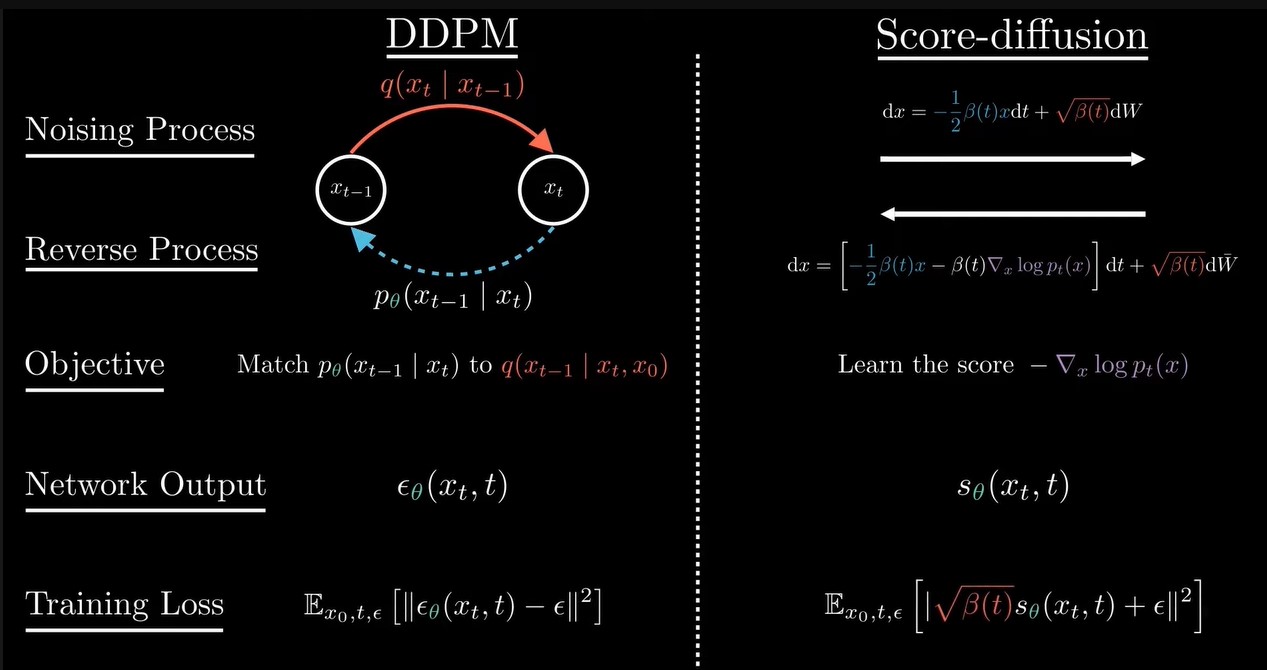
score based diffusion更general，可以选择不同的SDE方程，也可以用其他的离散化方法。